Thyrd: An Experimental Reflective Visual Programming Language

Philip J. Mercurio

Thyrd Informatics

mercurio@thyrd.org

 

 

ABSTRACT

This paper presents Thyrd, an experimental visual programming language and environment. The goal is a programming environment in the spreadsheet paradigm but built on a minimal set of constructs. In Thyrd, both data and code are stored in cells situated in nested two-dimensional grids. All editing operations are implemented as operators in the Thyrd language, thus Thyrd is reflective: a Thyrd program can inspect and modify itself or other programs in the same space.

Thyrd is a postfix concatenative language most similar to Joy[1]. The environment animates the stacks of a Thyrd program and allows the program to be stepped both forwards and, in limited cases, backwards.

Thyrd's tabular display may be overlaid with a panel consisting of arbitrary widgets editing the contents of individual cells or an entire grid. Each element of the user interface acts as a portal supporting inspection and modification of the underlying source code.

Thyrd is an open source community project available online at thyrd.org.

Categories and Subject Descriptors

D.1.7 [Programming Techniques]: Visual Programming; D.2.6 [Programming Environments]: Interactive environments; D.3.2 [Programming Languages]: Applicative (functional) languages, Concurrent, distributed, and parallel languages; H.4.1 [Office Automation] Spreadsheets.

General Terms

Languages, Theory.

Keywords: Visual programming, functional programming, interactive programming environments.

1.     INTRODUCTION

The most successful programming paradigm, at least in terms of popularity, is the spreadsheet [2]. Thyrd is an attempt to reduce the spreadsheet programming model to its minimal aspects by focusing on a small set of central concepts. In the process, we reify the code used in formulas so that it can be manipulated using the same mechanisms as those used to edit the spreadsheet itself, creating a reflective visual programming language. These reflective features also allow a user to manipulate the code for a formula using the same mechanisms used for manipulating data, smoothing the transition from user to programmer.

The language embodied in Thyrd is a concatenative (stack-based) language in the same family as Forth [3]. It most resembles Joy [1], a purely functional cousin of Forth. Like Joy, Thyrd implements iteration and recursion using quoted programs and combinators (higher-order functions) that operate on programs. To help the programmer understand a Thyrd program, a viewer is provided that animates the stacks. The viewer allows a program to be stepped forward and, in limited cases, backwards. This encourages an iterative style of programming where code that contains an error or is incomplete can be inspected, modified, and resumed from that point.

Thyrd attempts to move beyond the matrix presentation inherent in electronic spreadsheets by providing overlays called panels that can be comprised of any widgets. Panels can be specified for individual cells, selected based on the type of the data within the cell, or can overlay an entire grid, hiding all of the data and code beneath. In this manner, a user interface can be constructed for use by a non-programming end user. A programmer can then inspect that interface to uncover and modify the underlying data and code.

Thyrd is implemented in Tcl/Tk [4] and Poet [5] and available as open source from SourceForge.net. Thyrd adheres to the Tcl philosophy that all data values can be represented as a string, and uses Poet's type annotations to specify cell types, as described below.

The paper is structured as follows: Section 2 describes the language and its key concepts, while Section 3 describes the visual programming environment. Section 4 discusses programming in Thyrd, then Section 5 presents related work that informed the design of Thyrd and Section 6 concludes the paper.

2.     THE LANGUAGE

The runtime state of the Thyrd interpreter consists of: the space of nested cells, called Thyrdspace; a set of triads, which bind cells together in groups of three; and a set of waves, which are concurrent flows of execution traversing Thyrdspace. The cells and triads persist in Thyrd session files, while the internal states of waves are transient and are reinitialized when a session file is loaded into the interpreter.

2.1     Thyrdspace

The primary computational unit in Thyrd is the cell. Each cell contains one nucleus, or core, that holds the cell's data. A cell's core may be atomic, in which case it contains one value, or it may contain a two-dimensional array of cells, called a grid. Thyrd's view of an atomic cell is shown in Figure 1. The core (an integer with value 42) is shown in a white outlined field. A triad binding this cell to two other cells is shown below the core, as two portals that can be used to navigate to the other cells. (The three cells of a triad are labeled A, B, and Y, as described below.)

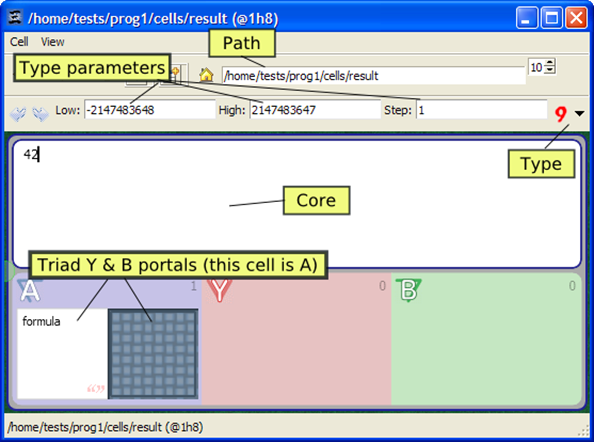
Figure 1: A view of an atomic cell

 

An atomic cell may contain a core of any type. The value of a core is a Tcl variable, as such it can always be represented as text. Internal to Tcl, however, it may also be stored as an integer, list, or some other representation based on its usage. Thyrd uses Poet's type annotations to express a recommended view of a core without imposing restrictions on the values it may assume. By default, a core is of type <string>, indicating that it is a string of Unicode characters. Types include primitives, such as <real>, <integer>, and <boolean>, and aggregates like <choice>. These annotations can be extended with optional parameters. For example, the type annotation <real> -1.0 1.0 0.1 indicates a real value ranging from -1.0 to 1.0 in increments of 0.1. A choice between three values would be specified as <choice> alpha beta gamma. (See the discussion of type annotations in [5].)

Type annotations are used to select an appropriate editing widget when panels are enabled. For example, a cell with a core of type <choice> would be rendered as a drop-down list of the possible values instead of an unadorned text entry widget.

A Thyrd cell establishes a location for a value and its relationships to other values, while allowing the core value to change and to assume different types. In the Thyrd interpreter, cells, not cores, are the unit of computation, thus all data references are call-by-name rather than call-by-value. When we state, in the discussion of waves below, that a value is pushed onto a stack, what's specifically happening is that a cell containing a value in its core is pushed onto the stack. This is analogous to a Forth-like language where the stack contains pointers to values rather than the values themselves.

2.2     Grids and Paths

One cell is designated as the root of the Thyrdspace hierarchy. Cells contained recursively within the root are said to be situated. Non-situated or free cells may still be attached to other cells via triads (see 2.3 below). A truly free cell not bound by any triads is subject to garbage collection.

All cells have a textual name (the name of the Poet object representing the cell—the Tcl equivalent of a pointer). Situated cells can also be addressed via a path that expresses how to navigate to the cell starting from the root. In Figure 1, the cell's path is /home/tests/prog1/cells/result and its name is @1h8. A cell's name is also a valid path to the cell, for both situated and free cells.

The axes of a grid are designated i and j and indexing begins with 0. The cells with i or j equal to 0 are the frame cells, the rest are the content cells. The text in the frame cells can be used to refer to a row or column, or numerical indexes may be used. If only the i index is given, the j index defaults to 1. The components of a path are separated by a '/' (forward slash) character.

In the grid shown in Figure 2, the cell containing the text two can be addressed as 2 1, 2, beta english, or beta. The cells containing the text alpha, beta, and gamma are the i frame, those containing english, spanish, and french are the j frame, and the 0 0 cell does not exist.

Figure 2: A grid cell

Note that if the frame cells are left empty and only the j = 1 cells are used, a grid becomes an ordered list of values that can be indexed using 1, 2, and so on. If only the i frame and j = 1 cells are used, the grid behaves as a list of key-value pairs. Nested grids can be used to represent a tree structure. Thus a Thyrd grid is a general data structure that subsumes lists, dictionaries, trees, and tables.

Paths beginning with / are absolute paths anchored at the root cell. Paths may also be specified relative to another cell using spatial indexing. The grid cell containing the current cell, and the cells containing it all the way up to the root, can be indexed by prefixing one or more periods, in a manner resembling file system paths in Unix and other operating systems. Given a starting cell, a relative path to its container is ../, while the container's container is ../../ or .../. One path from the two cell to the uno cell in the grid shown in Figure 2 would be ../alpha spanish.

Spatial indexing within a grid is supported by prefixing an index with - (minus) or + (plus). If followed by a numerical value, it indicates that many cells in the given direction, while a * indicates the spatial limits of the contents cells, - indicates the frame cell, and + indicates an index after the last cell in that direction (i.e., an index for a cell that does not yet exist). Examples of within-grid spatial indexes are shown in Table 1.

The various forms of spatial indexing, when used in a formula attached to a cell (see 2.4), allow the formula to be applied to multiple cells unmodified, avoiding the transformation of relative addresses that occurs when a formula in a VisiCalc-like spreadsheet is copied. In a typical spreadsheet, a cell at C4 refers to the cell immediately to its left as B4, while the cell to the left of C5 is B5. In Thyrd, the cell on the left is -1, regardless of the coordinates of the starting cell.

Table 1: Spatial indexing from the cell beta english in Figure 2.

2.3     Triads

In Thyrdspace, cells are bound together in sets of 3 called triads. A triad consists of three paths to cells: A, B, and Y. They can take on any meaning, but usually Y expresses the relationship between A and B. If thought of as a labeled directed graph, A is the head of an arc, B is the tail, and Y is the label.

The system maintains maps which facilitate retrieval of all of the triads attached to a given cell or pair of cells. Only one triad is allowed to exist between any triplet of cells, adding a triad whose paths resolve to three cells that are already bound together is a null operation.

A triad is used to specify an attribute of a cell A by binding it with an attribute name in Y and value in B. Thyrdspace contains a table, located at /thyrd/ys, containing Y cells used as attributes and specifying additional information about each, including a default value and type for the B cell, and help text describing the attribute. The table also associates a route, which is an ordered list of paths, with each attribute, specifying how the value of an attribute can be spatially inherited from other cells in the grid. For example, the route associated with the attribute width, which specifies the display width of a cell in pixels, consists of the two paths +0 -- and -- --. If a cell does not have a width attribute, the value is obtained from the i frame cell at the top of that column, or from the 0 0 cell. If neither of those cells contains a width setting, the default value is used. The programmer may add entries to the ys table to define additional attributes with spatial inheritance semantics.

Attributes that are currently defined in Thyrd include width and height, specifying the dimensions of the cell; panel, which specifies the widget to be used to edit a cell; and formula and event, which associate a cell with another cell containing executable code. A representation of a formula triad is shown in the lower left corner of Figure 1: the cell being viewed (/home/tests/prog1/cells/result) is A, and we see portals to the Y and B cells of that triad (the value of /thyrd/ys/formula is formula, and the crosshatch pattern to its right indicates a grid). In the cell editor, the user can click on the cells shown in a triad to navigate to them or open them in new windows.

 

2.4     Formulas and Events

There are two ways to bind a cell, called an anchor cell in this context, to another cell containing a Thyrd program. If the formula attribute is used, the associated code is evaluated and the resulting value is placed in the anchor cell. Whenever the cells in the formula change, or any other cells referenced by the formula change, the formula is reevaluated and the anchor cell is updated.

The event attribute is used to bind an anchor cell with a program that is executed only when the anchor cell changes value, independent of any other cells. Formulas use the anchor cell as output, and all the cells referenced by the formula are inputs that trigger recalculation, while events have only one input, the anchor cell. Formulas support declarative spreadsheet-like computations, while events support execution triggered by user interface actions.

 

2.5     Waves

Associated with each formula or event is an independent wave of execution that passes through Thyrdspace. A wave consists of paths to the anchor cell and the program, several stacks, and two routes. There are three data stacks labeled A, B, and Y—for most operations only one stack is used, but all three are used by operations that manipulate triads. The contents of the stacks are cells. If a raw value needs to be pushed onto a stack it is first wrapped in a free cell that will be garbage collected later (if it is still free).

There is also an execution stack, called X, which is initialized with the first cell of the program. Execution begins by popping the top cell of the X stack, if it contains an opcode it is executed, else it is pushed onto the currently selected data stack. Pushing a data cell and executing most opcodes leave the X stack empty, in which case the wave's next route is applied to the just-executed cell to obtain the next cell to be executed. The default route causes the program grid to be traversed from left to right, top to bottom. A wave also contains a previous route, used when executing a program in reverse. Either route can be modified by the program to implement any form of two-dimensional traversal.

Program 1a: A simple program

Program 1a is the formula for the cell shown in Figure 1. When initialized, the wave associated with this program has the first cell, the one containing the value 6, pushed onto the X stack. Execution begins by popping a cell off the X stack and executing it. Since it is a data cell, it is just pushed onto the A stack. The X stack is now empty, so the next route is used to find the next cell to execute. This cell is pushed on the X stack to complete one step in the execution of the program. Executing steps from multiple concurrent waves is managed by the Tcl event queue.

When the next step for this wave emerges from the event queue, the cell containing 7 will be pushed on the A stack, the X stack will again be empty, and the next route will be followed again to find the cell containing the multiply opcode. Any intervening empty grid locations are ignored—the route is applied repeatedly until it finds an occupied grid location—so we can lay out the cells in arbitrary ways. (Note: by empty grid locations we mean cells that are not present, not empty cells. An empty cell, if it's not an opcode, is an empty string and would get pushed on the stack. An opcode whose value is the empty string is the do nothing or no-op opcode.)

At the third step this wave would execute the multiplication opcode, popping two values off the A stack and pushing their product. Following the next route now fails to yield a cell, since we are at the end of the program. This causes an end opcode to be pushed onto the X stack and evaluated at the next step. end takes the top of the selected stack and uses it to set the anchor cell's value and type. A program can empty the selected stack before ending in order to leave the anchor cell unchanged.

Program 1b: A simple program, made complicated

Quotation is expressed by enclosing cells in a grid cell—when a grid cell is encountered on the X stack it is pushed, unmodified, onto the current data stack. Combinators are implemented as opcodes that manipulate the X stack. For example, evaluate, which executes a quoted program, pops a grid cell off the data stack and pushes its first content cell onto the X stack. This is used in the program in Program 1b. First the 6 is pushed, then a grid containing the 7 and multiply cells. evaluate pops the grid and pushes the 7 cell on the X stack, and execution continues in the same manner as in Program 1a.

Other simple combinators include the if then else opcode, which pops three items off the stack, a truth value and two quoted programs, then uses the truth value to determine which of the two quoted programs to unquote and push on the X stack.

Like Joy and other functional languages, Thyrd uses combinators to implement iteration and recursion. For example, repeat pops an integer n and a program, and evaluates the program n times. The fold opcode takes two parameters: a grid of values and a quoted binary operation (such as add or multiply), folds the binary operation in-between each pair of values in the grid, and evaluates the result to produce a single value. Recursion is handled by opcodes patterned after Joy's primitive and linear recursion combinators.

Program 2 uses the fold opcode and another combinator, step, to compute the average of a grid full of values. step evaluates a quoted program once for each cell in a grid. The first row in Program 2 retrieves a grid cell called input from two levels up and then duplicates it on the stack. The next row uses fold and add to compute the sum of the values in the input grid. The third row pushes a 0 value and then uses step to increment the value once for each cell in the input grid. The last row divides to get the average and then sets the type of the top cell, which the implicit end then uses to set the value and type of the anchor cell.

Program 2: Computing an average.

 

It is difficult to represent Thyrd programs effectively in a single image. The reader is encouraged to view the screencasts at http://thyrd.org/thyrd to get a better feel for Thyrd programming.

Each of a wave's four stacks has a corresponding history stack used when the wave is enabled for bidirectional execution. Operands and opcodes popped off the main stacks are pushed onto the matching history stacks where they can be recalled if execution is reversed. Work is ongoing to implement bidirectionality for the general case, but the opcodes which edit Thyrdspace (cut, copy, paste, etc.) are bidirectional.

 

Thyrd uses a bidirectional wave internally to implement undo and redo of editing operations. The editing controls cause editing opcodes to be pushed onto the stacks of this wave and executed. The undo and redo buttons step the execution of this wave backwards and forward.

 

3.     THE ENVIRONMENT

Thyrd begins with a small toolbox window with buttons for opening instances of the main editing windows. The toolbox includes a large start/stop button that enables/disables the execution of all programs. The size and location of the toolbox and other windows is stored within Thyrdspace itself, so that, when a Thyrdspace file is reopened, all of the windows' positions are restored. This also means that windows can be created, moved, and resized by a Thyrd program.

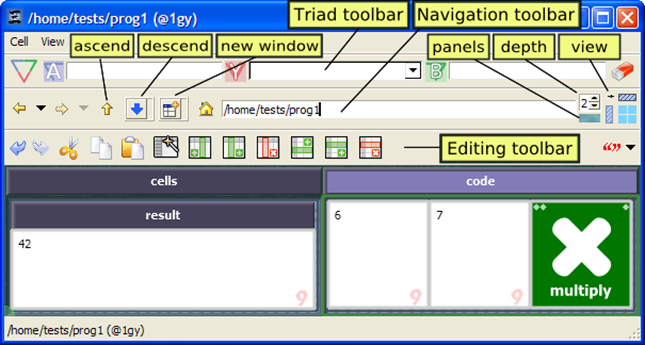
Figure 3: The cell editor viewing a grid with all toolbars enabled and depth set to 2.

3.1     Cell Editor

Most interaction in Thyrd occurs in a cell editor, already shown in Figure 1 but shown in more detail, and with all toolbars enabled, in Figure 3. The top toolbar has three fields where cell paths can be entered or dropped, and a button to bind the three paths in a triad. This toolbar is not frequently used and is usually not displayed, since most triads are formed by other actions in the interface. For example, the width and height of cells are set by directly manipulating the boundaries of the frame cells.

The second toolbar is the navigation toolbar and is normally displayed. The main controls are the text entry editing the path to the displayed cell and the backwards and forward history buttons, supporting navigation similar to that found in a web browser.

This toolbar includes controls to ascend and descend. Navigating up and down in the hierarchy is smoothly animated, zooming out or into the selected cell in about a second, in an attempt to keep the user oriented within the cell hierarchy.

At the right end of the navigation toolbar is a cluster of controls that affect how a grid cell is displayed. The depth control selects how many levels of the cell hierarchy to display. The view cluster controls whether or not the frame cells are shown, whether the i axis extends to the right or downward, and the layout of cells (fixed-width vs. expanded). The panels button toggles the display of overlay panels, discussed below.

The bottom toolbar contains the editing controls, with undo/redo controls at the far left. At the far right of the editing toolbar is a drop-down menu used to set the type of the selected cells.

In each cell of the grid, the value is shown as text and the type is shown as an icon in the lower right corner. The text may be edited freely, validation and propagation of the changed value does not occur until a confirmation button is pressed. Clicking on the cell background begins cell selection, clicking on the type icon begins a drag-and-drop operation that can be used to copy the cell's contents to another cell or copy the path to a drop target. Moving the mouse into a cell causes its path to be shown in the lower left corner of the editor window.

3.2     Panels

Panels, which are arbitrary user interfaces implemented in Tcl and can thus contain any widgets available in Tk or its many extensions, can be specified by setting the panel attribute of a cell. Cells can spatially inherit their panel attribute from their associated frame cells, so that panels can be specified for content cells before they are created. There are two types of panels: atomic panels, which overlay individual cells as shown in a grid, and grid panels, which replace the entire cell editor display with a custom interface.

 

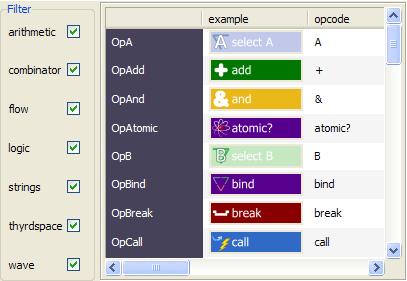
Figure 4: A filtering table panel

Figure 4 shows the /thyrd/ops grid, which contains information on all of Thyrd's opcodes, overlaid with a table interface with filtering capabilities. In the underlying grid, the opcode names are the i frame, and each j row contains an example of the opcode, its textual value and the caption on the icon, names for its in and out parameters, help information, and a set of tags categorizing the opcode. This panel flips the table so that the rows become columns, enables sorting by column, and examines the tags row of the grid to construct a checkbox for each tag used. Deselecting a tag removes the corresponding opcodes from the table without affecting the underlying grid's data. This particular window is a handy tool for the Thyrd programmer, since it documents the language and provides an example of each opcode that can be drag-and-dropped onto a program under construction, but the panel can be reused to display any grid. This panel is implemented in ~2000 lines of Tcl code and is selected by setting the cell's panel attribute to Table -readonly yes -flip yes -filter tags.

 

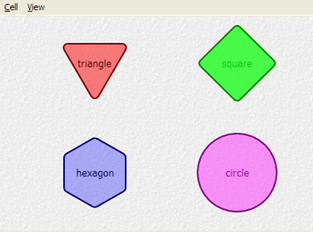
Figure 5: A drawing canvas panel

 

A panel need not resemble a table at all. Shown in Figure 5 is a panel that takes each row of the underlying grid as the specification for a figure to be drawn on a canvas. A view of the underlying data (i.e., the same cell with paneling turned off) is shown in Figure 6. Changes in the data are reflected in the canvas, and direct manipulation of the canvas items modifies the underlying data.

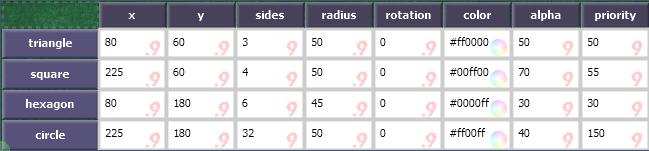
Figure 6: The data for Figure 5.

3.3     Wave Editor

The wave editor, the bottom window shown in Figure 7, is used to inspect waves of execution passing through Thyrdspace. At the left is a table of all of the waves that currently exist. The selected wave is shown to the right.

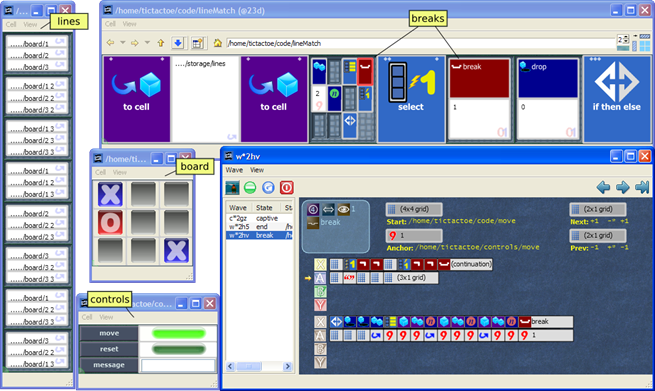
Figure 7: A Thyrd programming session

The wave editor shows the X, A, B, and Y stacks, followed by the corresponding history stacks. The cell at the top of each stack is shown in full, with the deeper cells represented by icons. Passing the mouse over a cell on a stack causes it to appear on top of the rest so its value can be seen. Cells can be dropped onto the navigation bar of a cell editor to open the cell for editing.

The arrows on the right of the wave editor's toolbar control stepping backwards and forwards through the program. The arrow at the far right causes a wave to run to the next breakpoint (or to the end) without stepping through it.

Determining which wave to select can be done in two ways. If a cell from a program is dropped onto the wave table, the wave corresponding to that program will be highlighted in red. Or, the user can activate the catch the next wave button shown at the left of the toolbar. This causes the next wave that starts to be selected automatically.

 

4.     PROGRAMMING IN THYRD

Figure 7 shows a Thyrd programming session during the development of a tic-tac-toe player. This example is much more complex than most Thyrd users would attempt, but it highlights several aspects of the Thyrd programming paradigm.

The top window shows the code under development, a portion of the tic-tac-toe AI that looks for lines containing a win for O or a win for X that must be blocked. The game board and control panel are grids covered by custom panels. The move and reset cells are anchors bound to event programs.

This portion of the program needs to model the game board as a set of lines—the 8 horizontal, vertical, and diagonal lines that form a win in tic-tac-toe. In a text-based language this would be modeled as an array of arrays, each representing one line via 3 indexes into the model of the board. The Thyrd representation, shown on the left in Figure 7, is conceptually similar: it is a grid of 8 subgrids, each containing 3 path cells indexing into the game board. However, the Thyrd lines model was constructed visually, by creating the empty grid structure then dragging each cell from the board to the correct spot in the lines grid. A new programmer trying to understand this program can inspect the model interactively to discover the relationship between the lines model and the game board.

The program shown in the top window contains two red break opcodes, one outlined in red. When a wave encounters a break it stops queuing new steps. The wave editor shows execution stopped at the outlined break. The programmer can now inspect the code and data stacks to investigate the current state of the program, inspect the history stacks to see what code has just been executed, and step the program forward and, for simple opcodes, backwards. The programmer can also modify or add code after the break and then continue from this point. A program can be constructed iteratively by starting with a single break, playing to that point, then adding and stepping through new instructions—essentially, programming by debugging the null program.

 

5.     RELATED WORK

In their HOPL III paper on Self [6], Ungar and Smith state that Smalltalk was striving to realize a Platonic ideal, an apotheosis, of object-oriented programming (p. 9-8). Self, in turn, was designed with an even more minimalist goal. The Thyrd project is motivated by a desire to see this minimalist approach applied to spreadsheet programming.

Boxer [7] is a visual structured programming environment for a Logo-like language that is a primary influence on the design of Thyrd. Boxer employs a spatial metaphor wherein the geometry of the presentation of the language, which consists of nested boxes, expresses the semantics of the language. Thyrd's panels are inspired by Boxer's ability to hide the code of a program behind its interface.

Forms/3 [8], a form-based, declarative visual programming language, is one of many investigations extending the boundaries of the spreadsheet genre and is also a major influence on Thyrd. Other examples include: Wizcell [9], in which cells can contain other cells and which, like ThingLab [10], uses paths to express containment. Thyrd implements only absolute and relative paths, compared to the four types of paths implemented in Wizcell. The WYSIWYC spreadsheet [11] uses the visible structure of the spreadsheet to express computational structure, replacing traditional text-based formulas. The intensional spreadsheet described in [12] implements spatial operators; Thyrd's spatial indexing is a similar approach. Spreadsheet 2000 [13] divides a spreadsheet into small sheetlettes joined by flow lines, just as Thyrd relies on multiple small grids instead of a single large sheet. Subtext [14] deviates further from the spreadsheet paradigm to explore the underlying simplicity of programming in an environment where the representation of a program is the same as its execution. Common to all of these sheet languages is a rejection of the standard approach to relative cell references found in VisiCalc [15] and its descendants.

There are many spreadsheets or spreadsheet-like systems that imbed a higher-order language for specifying formulas. Scheme is used in Siag [16], Haskell is used in Haxcel [17] and Vital [18], Clean is used in FunSheet [19], Python is used in Resolver One [20]. All of these systems allow advanced programming techniques, such as recursion, to be used in a spreadsheet environment. Although they use languages that support reflection, these spreadsheets do not reify code so that it can be manipulated by a spreadsheet program.

The Thyrd language is patterned after Joy, although the addition of optional type annotations for cells causes it to resemble Cat [21] as well. Thyrd is also influenced by two-dimensional programming languages such as Befunge [22] and Orthogonal [23]. The bidirectional execution support in Thyrd is based on RVM-Forth [24].

 

6.     CONCLUSION

By focusing the design of Thyrd on a small set of central concepts—cells, triads, and waves—we aim to create a live programming language that can be inspected and modified down to its lowest level. The addition of panels allows the underlying complexity to be obscured yet still accessible. While the stack-based language and nested grid structure might be harder to learn compared to their counterparts in a traditional spreadsheet, animation and direct manipulation are used in an effort to mitigate these difficulties. Thyrd currently exists as a research prototype, released as open source at http://thyrd.org/thyrd. Future efforts will focus on enhancing usability while maintaining Thyrd's fundamental simplicity and transparency.

 

7.     REFERENCES

[1]        M. von Thun. Joy: Forth's Functional Cousin. EuroForth 2001, Schloss Dagstuhl, Germany, November, 2001.

[2]        C. Scaffidi, M. Shaw, and B. Myers. Estimating the Numbers of End Users and End user Programmers. In Proceedings of the 2005 IEEE Symposium on Visual Languages and Human-Centric Computing (September 20 - 24, 2005). VLHCC. IEEE Computer Society, Washington, DC, 207-214.

[3]        E. Rather, D. Colburn, and C. Moore. The Evolution of Forth. In History of Programming Languages-II, Bergin T. J. and Gibson, R. G., Ed., New York NY: Addison-Wesley, 1996.

[4]        J. K. Ousterhout. Tcl and the Tk Toolkit. Addison-Wesley, Reading, MA, USA, 1994.

[5]        P. Mercurio. Poet: An OOP Extension to Tcl Supporting Constraints, Persistence, and End-User Modification. In Proceedings of Tcl'2007: The 14th Annual Tcl/Tk Conference, New Orleans, Louisiana, USA, September 2007. See also http://poet.sf.net

[6]        D. Ungar and R. Smith. Self. In Proceedings, History of Programming Languages Conference III, San Diego, California, USA, June 2007

[7]        A. diSessa. Models of computation. In D. A. Norman and S. W. Draper (Eds.), User Centered System Design: New Perspectives on Human-Computer Interaction. Hillsdale, NJ: Lawrence Erlbaum, 1986, pp. 201 - 218.

[8]        M. Burnett, J. Atwood, R. Djang, H. Gottfried, J. Reichwein, and S. Yang. Forms/3: A first-order visual language to explore the boundaries of the spreadsheet paradigm. Journal of Functional Programming, 11(2):155—206, March 2001

[9]        M. Montigel. Portability and Reuse of Components for Spreadsheet Languages. In Proceedings of the IEEE 2002 Symposia on Human Centric Computing Languages and Environments (HCC'02), Arlington, Virginia, USA, September, 2002.

[10]     A. Borning. The Programming Language Aspects of ThingLab; a Constraint-Oriented Simulation Laboratory, ACM Trans. on Programming Languages and Systems, 3(4), October 1981, pp. 353-387.

[11]     N. Wilde. A WYSIWYC (what you see is what you compute) Spreadsheet. In Proceedings 1993 Symposium on Visual Languages, Bergen, Norway, 1993, pp. 72-76.

[12]     W. Du, WW. Wadge. A 3D spreadsheet based on intensional logic. IEEE Software 1990; 7:78—89.

[13]     S. Wilson. Building a Visual Programming Language. MacTech 13:4, 1997.

[14]     J. Edwards. Subtext: Uncovering the Simplicity of Programming. In Proceedings of OOPSLA'05, San Diego, California, USA, 2005.

[15]     D. Bricklin. VisiCalc spreadsheet. Announced at National Computer Conference, New York City, New York, USA, June, 1979.

[16]     U. Eriksson. Scheme in a Grid, 1996. Online at http://siag.nu/siag

[17]     B. Lisper and J. Malmström. Haxcel: A Spreadsheet Interface to Haskell. In Proceedings, 14th International Workshop on the Implementation of Functional Languages, Madrid, Spain, September, 2002, pp. 206-222.

[18]     K. Hanna. Interactive Visual Functional Programming. In Proceedings, International Conference on Functional Programming '02, Pittsburgh, Pennsylvania, USA, October, 2002.

[19]     W. de Hoon, L. Rutten, and M. van Eeekelen. Implementing a functional spreadsheet in Clean. J. Functional Programming, 5(3):383-414, July 1995.

[20]     Resolver One, Resolver Systems Ltd. Online at http://www.resolversystems.com

[21]     C. Diggins. The Cat Programming Language. Online at http://www.cat-language.com

[22]     C. Pressey. Befunge, 1993. Wikipedia entry at http://en.wikipedia.org/wiki/Befunge

[23]     B. Raiter. Orthogonal. Online at http://www.mup petlabs.com/~breadbox/orth/home.html

[24]    W. Stoddart. RVM-Forth, a Reversible Virtual Machine. EuroForth 2004, Schloss Dagstuhl, Germany, November, 2004.